
It’s easy to find beauty in nature, in art, in architecture, in music. We simply look at a flower, or a painting, or listen to Beethoven’s Fifth Symphony, and we feel something shift around inside our chest that screams, “this is beautiful.” We seldom pause to think about why we find that beauty is not often equal, but the answer is quite simple: mathematics. A single, simple sequence of numbers can account for why we find Beethoven Five more beautiful than Twinkle Twinkle, or why certain, ancient buildings continue to be considered the most beautiful in the world. Even aspects of technology and science, from the structure of galaxies to planetary orbits, find their roots in this sequence of numbers. And it’s as simple as 1 + 1 = 2. This sequence of numbers, named the Fibonacci sequence, is the single mathematical root from which infinite amounts of beauty in our universe derive. Though there exists no concrete answer as to why, the far-reaching and breathtaking applications of the Fibonacci sequence influence the human idea of beauty more so than anything else. For the purpose of brevity, my main focuses will be the inherent mathematical properties of the Fibonacci sequence and Phi/phi, as well as their applications in architecture, music, and science.
Though short, Benjamin Arthur’s TED Talk (found to the right) on Fibonacci numbers outlines the magnificent basis on which the rest of this information stands.
The Fibonacci sequence is defined as a sequence of numbers, beginning with one, in which the previous two terms are added to create the next term, and is infinite in that it contains no upward boundary. The first few terms are:
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 ... ∞
We can see how quickly it grows. However, that primary pattern is expected, whereas one would expect nothing special or similar if the squares of the numbers are added. Let’s attempt it, anyway.
1 1 2 3 5 8 13 21 34 55 ...
1 1 4 9 25 64 169 441 1156 3025 ...
1 + 1 = 2
1 + 4 = 5
4 + 9 = 13
1 1 2 3 5 8 13 21 34 55 ...
As we can easily see, the squares of Fibonacci numbers additionally add up to other Fibonacci numbers (every other Fibonacci number, to be exact.) What happens when we attempt to add three consecutive Fibonacci squares, as a partial sums series?
1 + 1 + 4 = 6
1 + 1 + 4 + 9 = 15
1 + 1 + 4 + 9 + 25 = 40
1 + 1 + 4 + 9 + 25 + 64 = 104
1 + 1 + 4 = (2 x 3)
1 + 1 + 4 + 9 = (3 x 5)
1 + 1 + 4 + 9 + 25 = (5 x 8)
1 + 1 + 4 + 9 + 25 + 64 = (8 x 13)
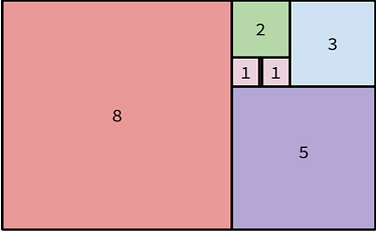
As we can see, while the sums are not directly Fibonacci numbers, they are the area of Fibonacci rectangles. Let’s look at this visually, in order to understand why this is the case.
Now, the connection becomes apparent. This is a common visual when exploring the Fibonacci sequence, though it commonly contains a spiral as well, or perhaps diagonals. Why? Because those additions create the most aesthetically pleasing ratios and patterns in all of the world. They are present in the Mona Lisa, in “The Creation of Adam,” in “The Annunciation”, and in the Sistine Chapel Ceiling. However, let’s look a bit more closely into the patterns that can be created using golden rectangles and ratios, so named for their seemingly divine beauty, specifically the harmonic sections of the Pantheon in Rome.
The Pantheon is arguably my favorite in the entire world, simply because it hides so much design and geometric complexity within a seemingly basic design. It holds a simple kind of elegance that radiates both power and beauty, a perfect analogy for the civilization that created it. This idea is supported by the harmonic sections created by using golden proportions and rectangles on the front of the Pantheon; though the sections are anything but obvious to the naked eye, focus on the symmetry and the location of important intersections with the border.
My analysis of the Pantheon involves only one construction, done many times to find the harmonic subdivisions of golden rectangles. The process is quite simple, as one must only find the golden rectangle, and construct many possible diagonals, as well as drawing the perpendicular and parallel lines to those diagonals. There are seemingly infinite possible harmonic subdivision patterns, but one appears obvious when observing the opening of the Pantheon. A simple, direct view of the building looks like this:
Once we draw the golden rectangle on the front facade of the building, we can essentially create whatever harmonic subdivisions we want. After playing around for a bit, I achieved this result, which I then overlayed onto the front of the building. Unfortunately, my focus on the golden ratio restricts me from discussing the large dome behind this opening, which was a gorgeous and extraordinary engineering feat, given the time of its construction.
However, the applications of the golden ratio stretch far beyond the likes of the Pantheon; the structure of the best music pieces, as well as the architecture of music theory itself, contains connections to the golden ratio and Fibonacci.
The most basic aspects of music theory are scales and chords. In western music, three main types of scales have dominated: the pentatonic scale, the diatonic scale, and the chromatic scale. The pentatonic scale, which contains five notes (the sharps or flats of an octave, or, as Garland points out, the black keys on a piano), composes the old folk tunes like “Amazing Grace” and “Mary Had a Little Lamb.” Conversely, the diatonic scale contains the other eight tones in an octave (the white keys), and composes most of the simple, classical melodies, the likes of Brahms’s “Lullaby” and “Row, Row, Row Your Boat.” If we combine the two, we achieve the thirteen-note chromatic scale, which composes most of modern music, including the great symphonies and contemporary music. What do these scales have in common? Fibonacci numbers: five, eight, and thirteen.
Oddly enough, the connection between Fibonacci and music only begins. Stradivari used the golden ratio to determine where to place the (eloquently nicknamed) f holes on the violin, as well as the proportion of size from the first, vaguely circular section to the larger, similar section, and the two most commonly used chords to resolve pieces, the minor and major sixth, have frequency ratios in notes which reduce to approximations of the golden ratio. These chords are thought to be some of the most pleasing to the ear, as well as the most aesthetically pleasing on the page. Lastly, some of the most prolific symphonies, such as Beethoven's Fifth and Ninth Symphonies and Mahler's Fifth Smphony, contain thematic structures whose time ratios are approximations of the golden ratio.
One of the other intriguing areas where Fibonacci numbers can be applied is in space, specifically the structure of galaxies and planetary orbits. The “systems of stars gathered together in a common plane, like those of the Milky Way” (Livio 120) contain the same logarithmic spiral patterns found in pineapples and sunflowers. What type of logarithmic spiral might this be? A golden spiral of course, which can be geometrically constructed using golden rectangles. Scientifically, the structure of galaxies retains a spiral shape due to the deflection of the “motion of stars and the glass clouds that generates the spiral density wave,” (Livio 122) due to irregular combinations of elliptic orbits. Imagine a perfect collection in which ellipses are placed inside each other like russian dolls, and then rotate each doll (ellipse) slightly, so that no orbit touches. It looks off-kilter, correct? This additionally is a way to create that logarithmic spiral Fibonacci loved so much.Given the connection of the rotation of galaxies to ellipses, it becomes more clear how planetary orbits connect to the golden spiral. However, Kepler, a famous Renaissance astronomer, applied his interest in both the planets and the golden ratio to prove that the area of distance between a planet and the sun that is created during a certain time interval of travel equals the other of the same length, no matter how far the planet is from the sun in its elliptical orbit. This is due to his earlier theorem that proves that planets move with greater speed when they are closer to the sun, so their base of travel is longer (with a shorter overall distance between the sun), but when the planet is farther away, the longer overall distance makes up for the shorter base.
So there it is: our galaxy’s construction in relation to the golden ratio in a nutshell.
We’ve examined how Phi creates gorgeous spirals, rectangle ratios, symphonies, and so much more, but we have yet to determine a basis for it. This was done on purpose, as I deliberately wanted to (1) make the math seem interesting before presenting the tough details and (2) save it for last, given that I’m unreasonably excited about this proof. In my calculus course, we’re working with infinite series and sequences, and how to determine whether they converge or diverge, and using this knowledge, I managed to apply it to the Fibonacci sequence in terms of the golden ratio.
HOW TO DERIVE BEAUTY FROM NUMBERS


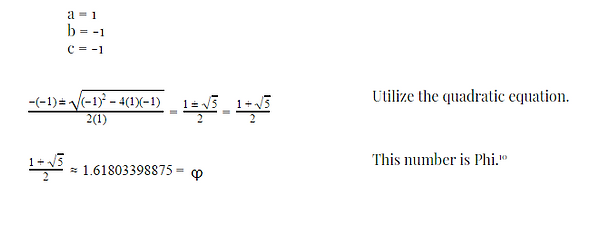


We look at a flower, or a painting, or listen to Beethoven’s Fifth Symphony, and we feel something shift around inside our chest that screams, “this is beautiful.” We seldom pause to think about why we find that beauty is not often equal, but the answer is quite simple: mathematics.



